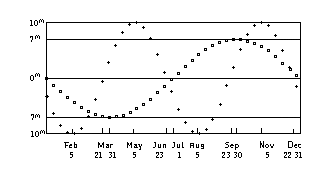
La variación de la Ecuación del Tiempo debida a la Oblicuidad (cruces)y a la variación debida al Movimiento Desigual (cuadrados).
Science and Engineering Research Council
Royal Greenwich Observatory
Cuaderno de Información No. 13: 'La Ecuación del Tiempo'
_________________________________________________________
La Ecuación del Tiempo:
La medición del tiempo ya no requiere relojes de sol sino que depende de dispositivos, tales como los relojes, para determinar una rata uniforme. Esta rata es calibrada usando observaciones astronómicas, para que la hora de los relojes sea equivalente al tiempo determinado por el movimiento promedio de la Tierra.
Sabemos, a partir de modernas observaciones astronómicas y observaciones de satélites artificiales, que la rata de rotación de la Tierra no es constante, sino que varía tanto en el corto plazo como a lo largo de los siglos. Estas pequeñas variaciones se deben a variaciones reales en la rotación de la Tierra, y son compensadas insertando segundos adicionales apropiadamente.
Si se usa un reloj de sol para determinar la hora, rápidamente se hace aparente que no indica la misma hora que los relojes. La diferencia asciende a unos 16 minutos en ciertas épocas del año. Esta diferencia también se nota como una falta de simetría en las horas de la salida y el ocaso del Sol. Se la llama La Ecuación del Tiempo.
La Ecuación del Tiempo tiene dos causas. La primera es que el plano del Ecuador de la Tierra está inclinado con respecto al plano de su órbita alrededor del Sol. La segunda es que la órbita de la Tierra alrededor del Sol es una elipse y no una circunferencia.
La Ecuación del Tiempo debida a la Oblicuidad:
El ángulo entre el plano del Ecuador y él de la órbita de la Tierra alrededor del Sol es llamado el ángulo de Oblicuidad (entre 21,55 y 24,18 grados).
Si asumimos que la órbita de la Tierra es circular, entonces el movimiento aparente del Sol a lo largo del gran círculo, o sea, la Eclíptica, será regular, cubriendo ángulos iguales en tiempos iguales. Medimos el tiempo aparente, sin embargo, como una proyección de este movimiento sobre el Ecuador [Celeste].
Esta proyección llegará a un máximo donde las tangentes a los grandes círculos del Ecuador y la Eclíptica estén paralelas (en los solsticios de verano e invierno, cerca del 21 de Junio y 22 de Diciembre) y llegará a un mínimo donde las tangentes los grandes círculos alcanzen su mayor ángulo (en los equinoccios, cerca del 21 de Marzo y 23 de Septiembre).
El Sol estará en el meridiano al mediodía en ambos solsticios y equinoccios y por lo tanto la
Ecuación del Tiempo debida a la Oblicuidad será cero en esos momentos.
Entre los solsticios y los equinoccios el Sol se retrasará con respecto a la hora del reloj, con
mínimos cerca del 5 de Febrero y del 5 de Agosto.
Entre los equinoccios y los solsticios el Sol se adelantará a los relojes, con máximos cerca del
5 de Mayo y del 5 de Noviembre.
La Ecuación del Tiempo debida al Movimiento Desigual:
La órbita de la Tierra alrededor del Sol es una elipse.
La distancia entre la Tierra y el Sol llega a su mínimo (perigeo) el 31 de Diciembre y es máxima
(apogeo) el 1 de Julio.
La Longitud aparente del Sol cambia más rápidamente cuando la Tierra está más cerca del Sol.
El Sol estará en el meridiano al mediodía en estas dos fechas y por lo tanto la Ecuación del
Tiempo debida al Movimiento Desigual será entonces cero.
Entre el 31 de Diciembre y el 1 de Julio el Sol se retrasará con respecto a la hora de los
relojes, con un mínimo cerca del 31 de Marzo.
Entre el 1 de Julio y el 31 de Diciembre el Sol se adelantará con respecto a la hora de los
relojes, con máximo cerca del 30 de Septiembre.
La variación de la Ecuación del Tiempo debida a la Oblicuidad (cruces)
y a la variación debida al Movimiento Desigual (cuadrados).
La Ecuación del Tiempo:
El total de estos dos efectos da la Ecuación del Tiempo,
que se define formalmente como la diferencia entre la hora de los relojes y la hora Solar aparente.
La Ecuación del Tiempo tiene la forma de la curva mostrada abajo.
Es cero en Abril 16, Junio 15, Septiembre 1, y Diciembre 25,
y tiene máximos y mínimos cerca de Febrero 12, Mayo 15, Julio 27, y Noviembre 4.
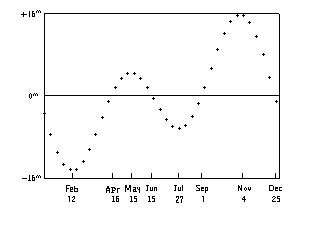La Ecuación del Tiempo (el total de los dos efectos de arriba).
Ver también; 'Relojes de Sol'
Producido por el Departamento de Servicios de Información del Royal Greenwich Observatory.
PJA Martes 25 de Noviembre, 13:18:49 GMT, 1993
webman@mail.ast.cam.ac.uk
Nota de ARVAL:
Si graficamos la Declinación del Sol versus la Ecuación del Tiempo para cada día del año, obtenemos el Analema; una figura que se encuentra en muchos relojes de Sol, mapas y globos geográficos.
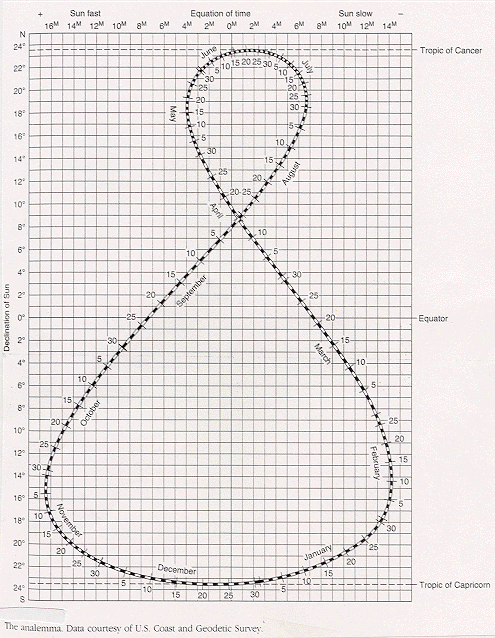
El Analema muestra que para todo sitio entre los trópicos de Cáncer y Capricornio (Lat. 23,45° N y 23,45° S) el Sol estará cenital dos veces por año. En el trópico de Cáncer, sólo en Junio 21. En el trópico de Capricornio, sólo en Diciembre 22. El Sol nunca estará cenital fuera de los trópicos.
También muestra que el Sol estará adelantado al reloj un máximo de 16 m 33 seg en Noviembre 3, y retrasado un máximo de 14 m 6 seg en Febrero 12.
Este Analema fue preparado para la Época 1950.
Para la Época 2000, la Ecuación del Tiempo es cero en Abril 15, Junio 13, Septiembre 1, y Diciembre 25,
y tiene máximos en Mayo 14 y Noviembre 3, y mínimos en Febrero 11 y Julio 26.
La Ecuación del Tiempo se corre 1 día en 24,5 años.
Ver Equation of time (Wikipedia, the free encyclopedia).
Ver Analemma (Bob Urschel)
Actualizada: Diciembre 20 '97, Junio 27 '14
Optimizada para ser vista en fuente Verdana.
Ver Sobre las Páginas en el Web del Observatorio ARVAL.
Regreso: ARVAL - Cuadernos del RGO
Mensajes: