Anterior: Planetas Arriba: El Sistema Solar Próximo: Datos del Sistema Solar

Órbitas

Royal Greenwich Observatory
_________________________________________________________

Cuaderno de Información No. 51: 'Órbitas'

Órbitas:

Hasta que Isaac Newton formuló sus leyes del movimiento, se pensaba generalmente que para mantener a un cuerpo en movimiento era necesario aplicar una fuerza para empujarlo o jalarlo. Esto estaba en buen acuerdo con la experiencia cotidiana según la cual las cosas se detienen cuando cesa la fuerza que las mueve. Galileo hizo una serie de experimentos que le llevaron a pensar que el movimiento era una propiedad intrínseca, que no requería mantenimiento, y Newton basó su teoría del movimiento en este concepto.
(En nuestra experiencia normal, el movimiento es frenado por la fricción o la resistencia del aire, que son fuerzas que deben ser balanceadas por una fuerza motriz para mantener el movimiento).

Las Leyes del Movimiento de Newton son;

1. Un cuerpo tiende a permanecer en movimiento, o detenido, a menos que sobre él actúe una fuerza.
2. La rata de cambio del momento de un cuerpo es igual a la fuerza que actúa sobre él.
   Esto hoy en día se expresa como; la fuerza que actúa sobre un cuerpo es igual al producto de su masa por su aceleración.
3. Para cada acción siempre hay una reacción opuesta y equivalente.

A partir de estas tres simples leyes, pueden deducirse todos los movimientos de los cuerpos bajo la acción de las fuerzas.
Newton mismo aplicó sus leyes al movimiento de los planetas y la Luna. Él se dio cuenta de que la gravedad era la fuerza que controlaba a los planetas y a la Luna en sus órbitas alrededor del Sol y de la Tierra.

Puede usarse un simple experimento para demostrar los principios de las órbitas controladas por la gravedad.
Tome un trozo de cuerda de 1 a 2 metros de largo y amarre un objeto de algún peso a un extremo.
Vaya a un área abierta, donde no pueda dañar algo, cuando el objeto vuele lejos de sus manos !
Si Ud. sujeta el extremo de la cuerda, y la hace girar a su alrededor, notará varias cosas:
Primero, sentirá que la cuerda jala en su contra, y que mientras más rápido la gire, más fuerte será la tracción.
También, notará que si suelta la cuerda, el objeto inmediatamente volará por la tangente, en línea recta.

Este simple experimento demuestra la primera ley de Newton; cuando Ud. no está ejerciendo un fuerza sobre el objeto, este viaja en línea recta.
También, la tercera ley; Ud. está jalando el objeto a través de la cuerda, y el objeto está también jalándolo a Ud.

También demuestra como un planeta es controlado por la atracción de la gravedad del Sol.
La velocidad del objeto determina la fuerza ejercida por la cuerda. Esto equivale, a que la velocidad de un planeta en su órbita está determinada por la atracción de la gravedad del Sol. Mientras más cerca esté un planeta del Sol, más fuerte será la atracción de la gravedad, y más rápidamente deberá girar el planeta para mantenerse en órbita.

Nota de ARVAL:
La ley de la Gravitación Universal de Newton es:

La interacción gravitacional entre dos cuerpos, puede expresarse por una fuerza de atracción central proporcional a las masas de los cuerpos, e inversamente proporcional al cuadrado de la distancia entre ellos.

F = G × m₁ × m₂ / r²

Donde G es aproximadamente igual a 6,674 × 10^-11   N × m² × kg^-2

F es medido en newtons (N), m₁ y m₂ en kilogramos (kg), r en metros (m)

Los planetas, sin embargo, no se mueven en órbitas circulares. Newton mostró que las leyes derivadas por Kepler estaban en acuerdo con su teoría, e indicaban que los planetas se mueven en órbitas elípticas alrededor del Sol.
Hoy en día podemos observar las órbitas con mucha exactitud y podemos tomar en consideración, no sólo la atracción gravitacional del Sol, sino también las mucho menores atracciones de los otros planetas.
Estos efectos hacen que los recorridos de los planetas se desvíen levemente de las elipses clásicas descritas por la simplificación de considerar sólo la atracción del Sol.

Nota de ARVAL:
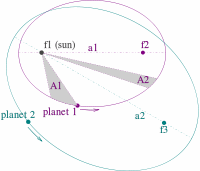
Las leyes de Kepler son:

1. Los planetas describen órbitas elípticas, con el Sol en uno de sus focos.
2. El vector de posición de cualquier planeta, relativo al Sol, barre áreas iguales de su elipse, en tiempos iguales.
3. Los cuadrados de los períodos de revolución, son proporcionales a los cubos de las distancias promedio al Sol.

1. Las órbitas son elipses, con focos f1 y f2 para el primer planeta y f1 y f3 para el segundo planeta. El Sol está en el punto focal f1.

2. Los dos sectores sombreados A1 y A2 tienen la misma área y el tiempo para que el planeta 1 cubra el segmento A1 es igual al tiempo para que cubra el segmento A2.

3. Los tiempos totales de órbita para el planeta 1 y el planeta 2 tienen una relación a1^3/2 : a2^3/2.

De Kepler's laws of planetary motion (Wikipedia)

La órbita de la Luna es especialmente compleja porque la atracción de la Tierra y la del Sol no son demasiado diferentes.
Es una sorpresa para muchos, que el recorrido de la Luna alrededor del Sol está siempre curvado en el mismo sentido, cóncavo hacia el Sol, y nunca hace lazos o es convexo hacia el Sol. Esto a pesar del hecho de que sabemos que orbita alrededor de la Tierra cada mes.

Uno de los grandes logros de la teoría de Newton, fue la determinación, por Halley, de que los cometas se mueven en órbitas elípticas o parabólicas.
Él calculó las órbitas de muchos cometas, y mostró que varios cometas supuestamente diferentes, seguían la misma órbita. Él conjeturó que eran el mismo objeto, y predijo que reaparecería en un año específico.
Ahora llamamos a este cometa con el nombre de Halley, en honor al hecho de que su análisis y predicciones eran correctas.

En la era moderna, hay muchos satélites artificiales en órbita alrededor de la Tierra, y sondas espaciales visitando los diferentes planetas y satélites del Sistema Solar.
El cálculo de sus órbitas y del recorrido de las sondas espaciales, es una compleja adaptación de la teoría derivada por Newton.

De la misma forma en que la Tierra está en órbita alrededor del Sol, el Sol está en órbita alrededor del centro de nuestra galaxia, la Vía Láctea.
El tiempo que toma una revolución es muy largo, cerca de 200.000.000 años, y el diámetro de la órbita es de cerca de 60.000 años-luz.

Glosario de términos:

Perigeo y Apogeo. Son la mínima y máxima distancias de la Tierra, de un satélite o de otro cuerpo.

Perihelio y Aphelio son la mínima y máxima distancias del Sol, de un satélite o de otro cuerpo.

La Excentricidad de una órbita es una medida de cuán distinta de un círculo es su forma.
Para una órbita circular, la excentricidad, (e), es cero, para una órbita parabólica e=1, mientras que una órbita hiperbólica tiene e mayor que 1.
Las órbitas elípticas tienen sus excentricidades mayores que cero, pero menores que 1.

Los Nodos de una órbita son los lugares donde la órbita intersecta algún plano fundamental.
Por ejemplo, los nodos de la órbita de la Luna alrededor de la Tierra, ocurren donde su órbita cruza el plano de la órbita de la Tierra alrededor del Sol.
La Luna debe estar cerca de uno de sus nodos en Luna Nueva o Llena, para que un eclipse de Sol o de Luna pueda ocurrir.

Órbitas Geosincrónicas, son aquellas en las que un satélite artificial en órbita alrededor de la Tierra, tiene un período de exactamente un día.
Esto significa que está siempre sobre el mismo lugar sobre el Ecuador de la Tierra.
Para los satélites en órbita cerca de 100 millas (160 Kilómetros) sobre la superficie, el período de revolución es de cerca de 90 minutos.
A medida que la altura de la órbita sobre la Tierra aumenta, disminuye la fuerza de atracción de la gravedad, la velocidad del satélite disminuye, y su período de revolución aumenta.
A una altura de 35.900 Km., el período orbital de un satélite en una órbita circular, es de un día, y permanece sobre el mismo punto del Ecuador Terrestre. Llamamos a esta órbita, geoestacionaria o sincrónica.

Producido por el Departamento de Servicios de Información del Royal Greenwich Observatory.

PJA Martes Mayo 8, 16:10:38 GMT 1996

Actualizada: Marzo 23 '97, Agosto 22 '13, Junio 24 '14

Optimizada para ser vista en fuente Verdana.
Ver Sobre las Páginas en el Web del Observatorio ARVAL.

Regreso: ARVAL - Cuadernos del RGO - El Sistema Solar